位置向量
外观
(重定向自向径)

位置向量(position vector,location vector,radius vector)又稱向徑、矢徑[1]、位矢[2],是几何学中用来表示空间裡某质点或物体相对于某参考点的“几何位置”的向量。
設定一坐标系,參考这坐标系,质点或物体的坐标,就是相对于這坐标系的原点的位置向量。在运动学裏,位置向量是描述质点运动的基本参量,是一个向量:有大小,也有方向。
位置向量
[编辑]从坐标原点指向质点所在位置的向量称为位置向量,亦稱位置矢量,简称位矢。
选定参考系,质点的位置由原点到质点的位置向量表示,随著时间的演化,位置向量可以描述质点的运动。在力学裏,位置向量常被用来跟踪质点、粒子、或刚体的运动。
微分几何用位置向量函数来描述连续性可微分曲线,其独立参数可以是时间,角度,或曲线径长。
不同坐标系中的位置向量
[编辑]
二维坐标系
[编辑]三维坐标系
[编辑]位置向量的导数
[编辑]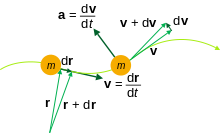
位置向量的改变称为位移,就是质点移动后的位置向量减去移动前的位置向量。位置向量對於时间的的导数称为速度向量:
位置向量對於时间的二阶导数称为加速度向量:











