位置向量
外觀

位置向量(position vector,location vector,radius vector)又稱向徑、矢徑[1]、位矢[2],是幾何學中用來表示空間裡某質點或物體相對於某參考點的「幾何位置」的向量。
設定一坐標系,參考這坐標系,質點或物體的坐標,就是相對於這坐標系的原點的位置向量。在運動學裏,位置向量是描述質點運動的基本參量,是一個向量:有大小,也有方向。
位置向量
[編輯]從坐標原點指向質點所在位置的向量稱為位置向量,亦稱位置矢量,簡稱位矢。
選定參考系,質點的位置由原點到質點的位置向量表示,隨著時間的演化,位置向量可以描述質點的運動。在力學裏,位置向量常被用來跟蹤質點、粒子、或剛體的運動。
微分幾何用位置向量函數來描述連續性可微分曲線,其獨立參數可以是時間,角度,或曲線徑長。
不同坐標系中的位置向量
[編輯]
二維坐標系
[編輯]三維坐標系
[編輯]位置向量的導數
[編輯]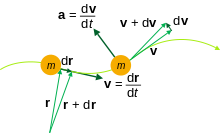
位置向量的改變稱為位移,就是質點移動後的位置向量減去移動前的位置向量。位置向量對於時間的的導數稱為速度向量:
位置向量對於時間的二階導數稱為加速度向量:











