非線性控制

回授控制系統，目的是控制一系統（受控系統）使其輸出可以追隨參考信號。感測器會將輸出轉換為信號，而控制器會將實際輸出的感測信號減去參考信號，應用所得到的誤差信號來控制受控系統，使其輸出接近參考信號。在非線性控制系統中，受控系統、感測器或是控制器中至少有一個是非線性的。

非線性控制（Nonlinear control）是控制理论中處理非線性系統的理論。控制理论本身是工程和数学的跨領域學科，探討动力系统在有輸入下的行為，以及如何利用反馈、前馈、信號濾波來改變輸入，以調整動力系統的輸出。被控制的系統會稱為受控體。有一個讓受控體輸出可以追隨參考信號的方法，就是將受控體輸出反馈到控制器，和參考信號比較，利用比較後的結果來改變受控體的輸入，使輸出可以追隨參考信號。

控制理论可以分為二種：線性控制理論可適用於元件均滿足叠加原理的系統（線性系統），其統御方程是線性的微分方程，線性系統中若其參數不會隨時間而改變，則稱為线性时不变（LTI）系統，這類系統可以用強大的頻域數學技巧加以分析，例如拉普拉斯变换、傅里叶变换、Z轉換、波德圖、根軌跡圖及奈奎斯特稳定判据。

非線性控制理論則是針對不符合叠加原理的系統（非線性系統），適用於較多的真實世界系統，因為所有真實世界的系統都是非線性的。其統御方程是非線性微分方程，要處理非線性控制的理論比較嚴謹，也比較不具一般性，只能適用在一些特定種類的系統。這些技術包括极限环理論、庞加莱映射、李亞普諾夫函數及描述函數。若只需要研究非線性系統在某穩定點附近行為，可以用近似的方式將非線性系統線性化，方法是將非線性解表示為無窮级数，再利用線性的技巧來處理。非線性系統一般會用電子計算機中的數值方法來分析，例如用仿真語言來仿真其行為。有時雖然受控體是線性的，但使用非線性控制會讓實現更簡單、速度更快、更準確、或是控制需要的能量更少，不過在設計上可能也會比較困難。

非線性控制系統的例子是自動調溫器控制的加熱系統。大樓的溫控系統對溫度的變化有非線性的響應，可能是「開啟」或是「關閉」，不像線性比例控制的設備，可以針對溫度差作較精細的控制。因此，溫度需低於「開啟」的設定溫度後，加熱系統才會打開，之後因為加熱系統的作用，溫度會開始上昇，溫度高於「關閉」的設定溫度後，加熱系統會關閉，溫度漸漸下降。加熱系統就會依此循環運作。這個溫度的循環稱為极限环，就是非線性系統的特點之一。

非線性系統的特點

以下是一些非線性系統的特點

• 不遵守叠加原理
• 有多個獨立的平衡點
• 會有像极限环、分岔、混沌的特性。

非線性系統的分析及控制

有許多針對非線性系統的分析及控制技巧：

• 描述函數法
• 相平面法
• 李雅普诺夫稳定性分析
• 奇异摄动法
• 針對絕對穩定性的波波夫判據及圓判據
• 中心流形定理
• 小增益定理
• 耗散性分析（Passivity analysis）

也有一些針對非線性系統的控制器設計技巧，可以分為幾類。一類是在可線性的範圍內，將非線性系統近似為線性系統，再用線性系統的方法處理：

• 增益規劃

也有一些是用輔助的非線性回授，設法讓系統接近線性，以設計控制器：

• 回授線性化

以及李亞普諾夫系列的方法：

• 李亞普諾夫再設計
• 控制李亞普諾夫函數
• 非線性阻尼（Nonlinear damping）
• 反演控制
• 滑動模式控制

非線性回授分析–Lure問題

Lure問題的方塊圖

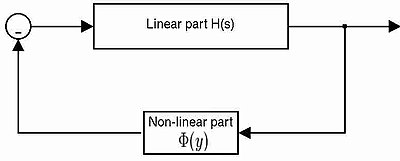
早期有一個由Anatoliy Isakovich Lure提出的非線性回授系統分析問題。

Lur問題描述的控制系統有一個線性非時變的前向路徑，其回授路徑有無記憶，可能時變的非線性成份。

其線性部份可以表示為四個矩陣(A,B,C,D)，非線性成份是Φ(y)，其中${\frac {\Phi (y)}{y}}\in [a,b],\quad a<b\quad \forall y$（扇形非線性）

絕對穩定性問題

考慮：

1. (A,B) 有可控制性，(C,A) 有可觀察性
2. 存在二個實數a, b，a < b，定義了Φ的扇形區域

Lure問題（也稱為絕對穩定性問題）是要推導只和傳遞矩陣H(s)和{a,b}有關的條件，可以使x = 0是系統的全域均勻漸近穩定平衡點。

有二個有關絕對穩定性問題的著名猜想，都已證實不成立：

• 阿依熱爾曼猜想
• 卡爾曼猜想

以圖形上來看，上述猜想可以表示為在Φ(y) x y或是dΦ/dy x Φ/y圖上的幾何制。這兩個猜想存在反例，在線性穩定扇形區域內存在非線性回授，使得穩定的平衡點和穩定的周期解同時存在（隱蔽振盪）。

有二個有關Lure問題的主要定理，提供絕對穩定的充份條件：

• 圓判據（線性系統中奈奎斯特稳定判据的延伸）
• 波波夫判據

在非線性控制中的理論成果

弗罗贝尼乌斯定理

弗罗贝尼乌斯定理是微分幾何中深刻的成果，其相關的概念和其他數學領域有關。若應用在非線性控制，其型式如下：假設以下型式的系統

${\dot {x}}=\sum _{i=1}^{k}f_{i}(x)u_{i}(t)\,$

其中$x\in R^{n}$，$f_{1},\dots ,f_{k}$是屬於$\Delta$分佈的向量場，而$u_{i}(t)$是控制函數，$x$的積分曲線會限制在$m$維流形，若$\operatorname {span} (\Delta )=m$，且$\Delta$是對合分佈。

相關條目

• 反馈钝化
• 锁相环
• 小控制信號特性

延伸閱讀

• Lur'e, A. I.; Postnikov, V. N. К теории устойчивости регулируемых систем [On the Theory of Stability of Control Systems]. Prikladnaya Matematika I Mekhanika. 1944, 8 (3): 246–248 （俄语）. 
• Vidyasagar, M. Nonlinear Systems Analysis 2nd. Englewood Cliffs: Prentice Hall. 1993. ISBN 978-0-13-623463-0. 
• Isidori, A. Nonlinear Control Systems 3rd. Berlin: Springer. 1995. ISBN 978-3-540-19916-8. 
• Khalil, H. K. Nonlinear Systems 3rd. Upper Saddle River: Prentice Hall. 2002. ISBN 978-0-13-067389-3. 
• Brogliato, B.; Lozano, R.; Maschke, B.; Egeland, O. Dissipative Systems Analysis and Control 2nd. London: Springer. 2007. 
• Leonov G.A.; Kuznetsov N.V. Algorithms for Searching for Hidden Oscillations in the Aizerman and Kalman Problems (PDF). Doklady Mathematics. 2011, 84 (1): 475–481 [2019-04-03]. doi:10.1134/S1064562411040120. （原始内容存档 (PDF)于2016-03-04）. 
• Bragin V.O.; Vagaitsev V.I.; Kuznetsov N.V.; Leonov G.A. Algorithms for Finding Hidden Oscillations in Nonlinear Systems. The Aizerman and Kalman Conjectures and Chua's Circuits (PDF). Journal of Computer and Systems Sciences International. 2011, 50 (5): 511–543 [2019-04-03]. doi:10.1134/S106423071104006X. （原始内容存档 (PDF)于2016-03-04）. 
• Leonov G.A., Kuznetsov N.V. Sergio, Bittanti , 编. Analytical-numerical methods for investigation of hidden oscillations in nonlinear control systems (PDF). IFAC Proceedings Volumes (IFAC-PapersOnline). Proceedings of the 18th IFAC World Congress. 2011, 18 (1): 2494–2505 [2019-04-03]. ISBN 9783902661937. doi:10.3182/20110828-6-IT-1002.03315. （原始内容存档 (PDF)于2020-07-09）. 

外部連結

• Wolfram language functions for nonlinear control systems （页面存档备份，存于互联网档案馆）