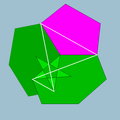
二十面化截半大十二面體

二十面化截半大十二面體

類別	均勻星形多面體
對偶多面體	內側二十角星化六十面體
識別
名稱	二十面化截半大十二面體 icosidodecadodecahedron icosified dodecadodecahedron
參考索引	U44, C56, W83
鮑爾斯縮寫	ided
數學表示法
考克斯特符號
威佐夫符號	5/3 5 | 3
性質
面	44
邊	120
頂點	60
歐拉特徵數	F=44, E=120, V=60 （χ=-16）
組成與佈局
面的種類	12個正五邊形 12個正五角星 20個正六邊形
頂點圖	5.6.5/3.6
對稱性
對稱群	Ih, [5,3], *532
圖像
5.6.5/3.6 （頂點圖） 內側二十角星化六十面體 （對偶多面體）

二十面化截半大十二面體（icosified dodecadodecahedron）又稱二十面十二面十二面體（icosidodecadodecahedron）是一種星形均勻多面體，由12個正五邊形、12個正五角星和20個正六邊形組成，索引為U₄₄，對偶多面體為內側二十角星化六十面體，其外觀與斜方截半大十二面體類似，差別只在正方形面被替換為正六邊形面，並且可以視為是斜方截半大十二面體的刻面多面體。

性質

二十面化截半大十二面體共由44個面、120條邊和60個頂點組成。在其44個面中，有12個正五邊形面、12個正五角星面和20個正六邊形面。在其60個頂點中，每個頂點都是2個六邊形、1五邊形和1個五角星的公共頂點，並且這些面在構成頂角的多面角時，以五邊形、六邊形、五角星和六邊形的順序排列，在頂點圖中可以用(5.6.5/3.6)或(6.5/3.6.5)來表示。

表示法

二十面化截半大十二面體在考克斯特—迪肯符號中可以表示為（o5/3x3x5*a）或（x5/4o5/2x3*a），在威佐夫記號中可以表示為5/3 5 | 3。

尺寸

若二十面化截半大十二面體的邊長為單位長，則其外接球半徑為七的平方根的一半：

$R={\frac {\sqrt {7}}{2}}\approx 1.3228756555$

邊長為單位長的二十面化截半大十二面體，中分球半徑為六的平方根的一半：

$R_{M}={\frac {\sqrt {6}}{2}}\approx 1.224744871$

二面角

二十面化截半大十二面體共有兩種二面角，分別為六邊形面和五邊形面的二面角以及六邊形面和五角星面的二面角。

其中，六邊形面和五邊形面的二面角角度約為100.8123度：

$\arccos \left(-{\frac {\sqrt {15\left(5-2{\sqrt {5}}\right)}}{15}}\right)\approx 1.759506857578\approx 100.812316964^{\circ }$

而六邊形面和五角星面的二面角角度約為37.377度：

$\arccos \left({\frac {\sqrt {15\left(5+2{\sqrt {5}}\right)}}{15}}\right)\approx 0.652358139784\approx 37.377368^{\circ }$

分類

由於二十面化截半大十二面體的頂點圖為交叉梯形且具備點可遞的特性，同時，其存在自相交的面，因此二十面化截半大十二面體是一種自相交擬擬正多面體（Self-Intersecting Quasi-Quasi-Regular Polyhedra）。自相交擬擬正多面體一共有12種，除了小雙三角十二面截半二十面體外，其餘由阿爾伯特·巴杜羅（Albert Badoureau）於1881年發現並描述。

自相交擬擬正多面體
（Self-Intersecting Quasi-Quasi-Regular Polyhedra）

小立方立方八面體	大立方截半立方體	非凸大斜方截半立方體	小十二面截半二十面體
大十二面截半二十面體	小雙三角十二面截半二十面體	大雙三角十二面截半二十面體	二十面化截半大十二面體
小二十面化截半二十面體	大二十面化截半二十面體	斜方截半大十二面體	非凸大斜方截半二十面體

相關多面體

二十面化截半大十二面體與10和20複合三角柱共用相同的頂點佈局。同時，其亦與斜方二十面體和斜方截半大十二面體共用相同的邊佈局。

凸包	斜方截半大十二面體	二十面化截半大十二面體
斜方二十面體	十複合三角柱	二十複合三角柱

參見

• 均勻多面體列表
• 扭稜二十面化截半大十二面體