貝特公式

貝特公式描述了 帶電粒子(質子，$\alpha$粒子，離子)穿越介質單位距離時的平均能損，即材料的阻止本領。 對於電子來說，其能損稍有不同，主要是由於其質量較小(要求相對論更正)以及其全同性，並且由於電子的軔致輻射損失能量較多，因此也需要將這一項考慮在內。快速的帶電粒子穿過材料時，與材料中原子的電子發生相互作用，從而激發或者電離材料原子，這一相互作用導致粒子的能量損失。

非相對論的貝特公式由漢斯·貝特在1930年發現，而相對論版(見下文)由他在1932年發現。注意平均能損不同於最可幾能損，後者由郎道-瓦維洛夫理論描述。

貝特公式有時被稱為貝特-布洛赫公式，但這是一種誤導(見下文)。

公式內容

速度為$v$，電荷數為$z$(整數，單位為基本電荷)，能量為$E$的帶電粒子，在電子數密度為$n$，平均激發能為$I$的材料中穿越距離$x$時，在國際單位制中，相對論版的貝特公式為：

$-\left\langle {\frac {dE}{dx}}\right\rangle ={\frac {4\pi }{m_{e}c^{2}}}\cdot {\frac {nz^{2}}{\beta ^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}c^{2}\beta ^{2}}{I\cdot (1-\beta ^{2})}}\right)-\beta ^{2}\right]$

1

其中c 是光速，$\varepsilon _{0}$為真空介電常數， $\beta ={\frac {v}{c}}$， $e$ 和 $m_{e}$為基本電荷和電子的靜質量。

停電的鋁用於質子和質子能，以及貝特的公式，而(紅色)和更正(藍色)

材料的電子數密度$n$可以通過下面公式來計算：

$n={\frac {N_{A}\cdot Z\cdot \rho }{A\cdot M_{u}}}\,,$

其中 $\rho$ 是材料的密度， $Z$ 是材料的原子序數，$A$ 是相對原子質量，$N_{A}$ 是阿伏伽德羅常數，$M_{u}$ 為摩爾質量常數。

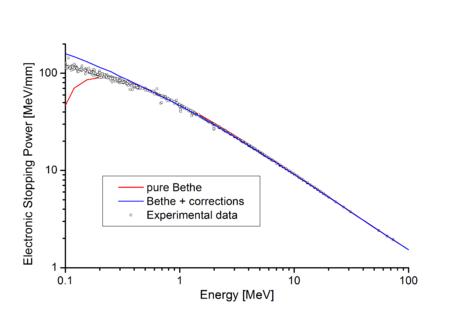
在右圖中，黑色圓圈是不同作者給出的實驗測量結果，紅色曲線是未修正的貝特公式。 顯然，貝特公式在高能區很好地符合了實驗結果。 當添加了一些修正項後，貝特公式符合得更好(圖中的藍色曲線，見下文)。

對於低能帶電粒子，即相對速度 $\beta \ll 1$，貝特公式簡化為

$-\left\langle {\frac {dE}{dx}}\right\rangle ={\frac {4\pi nz^{2}}{m_{e}v^{2}}}\cdot \left({\frac {e^{2}}{4\pi \varepsilon _{0}}}\right)^{2}\cdot \left[\ln \left({\frac {2m_{e}v^{2}}{I}}\right)\right].$

2

這可以從 (1)式中將 $\beta c$ 由 $v$ 替代，並忽略其餘 $\beta ^{2}$ 項得到。

在低能區，根據貝特公式，粒子的能損隨 $v^{2}$ 的增加而降低，並在 $E=3Mc^{2}$ 達到最小值，其中 $M$ 是粒子的質量(對於質子來說，該極值點約為3000 MeV)。 在極端相對論的情況下，$\beta \approx 1$，粒子的能損對數增加，這主要是由於電場的橫向分量造成的。