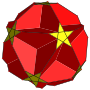
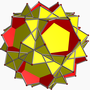
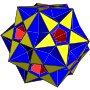
小复杂斜方截半二十面体
 | ||
| 类别 | 退化均匀星形多面体 | |
|---|---|---|
| 识别 | ||
| 名称 | 小复杂斜方截半二十面体 | |
| 鲍尔斯缩写 | sicdatrid | |
| 数学表示法 | ||
| 考克斯特符号 | ||
| 施莱夫利符号 | t0,2{5/2,3} | |
| 威佐夫符号 | 5/2 3 | 2 | |
| 性质 | ||
| 面 | 62 | |
| 边 | 120 | |
| 顶点 | 20 | |
| 欧拉特征数 | F=62, E=120, V=20 (χ=-38) | |
| 组成与布局 | ||
| 面的种类 | 20个正三角形 12个五角星 30个正方形 | |
| 面的布局 | 20{3}+12{5/2}+30{4} | |
| 顶点图 | 3(3.4.5/2.4) | |
| 对称性 | ||
| 对称群 | Ih, [5,3], *532 | |
| 图像 | ||
| ||
在几何学中,小复杂斜方截半二十面体是一种退化的星形均匀多面体[1],由20个正三角形、12个五角星和30个正方形组成,其可以视为大二十面体透过离面(Cantellation)或扩展(Expansion)变换而成,其外观与小双三斜三十二面体和五复合立方体所形成的复合几何形状相同[2]。
性质
[编辑]小复杂斜方截半二十面体是一种退化的均匀多面体,共有62个面、120条边和20个顶点,其顶点以每三个一组为单位互相重合[2]、其边为每两两一组为单位互相重合[2]。
面的组成
[编辑]小复杂斜方截半二十面体由20个正三角形、12个五角星和30个正方形组成,且面在顶点周围的分布为:每个顶点都是五角星、正方形、三角形和另外一个正方形的公共顶点,并且同时有三组相同结构,在顶点图中可以用3[5/2,4,3,4]表示[2],其中5/2表示五角星、4表示正方形、3表示正三角形[3]。
 构成小复杂斜方截半二十面体的五角星面 |
 构成小复杂斜方截半二十面体的正三角形面 |
 构成小复杂斜方截半二十面体的正方形面 |
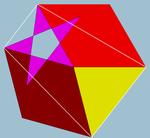 构成小星形截角十二面体的面在顶点周围的排布 |
相关多面体
[编辑]大复杂斜方截半二十面体
[编辑]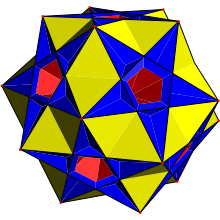
在拓朴学中,小复杂斜方截半二十面体与大复杂斜方截半二十面体拓朴同构。小复杂斜方截半二十面体可以透过将五角星面替换成五边形面拓朴变形而得。[2][4]大复杂斜方截半二十面体的外观与大双三斜三十二面体和五复合立方体所形成的复合几何形状相同[4]。
倒角大二十面体
[编辑]小复杂斜方截半二十面体可以经由大二十面体透过与正二十面体变换成小斜方截半二十面体相同的多面体变换变换而成[5],该种变换有时称为离面(Cantellation)或扩展(Expansion)[6],该变换也可以视为先倒角再截角[7],因此倒角大二十面体可以视为小复杂斜方截半二十面体截角变换的原像。倒角大二十面体与倒角大二十面体则为与五角星相邻的面被延伸到相交形成底面为五角星的锥体替换之。
 倒角大二十面体 |
 截角的倒角大二十面体 |
 倒角大二十面体的面 青蓝色为三角形面 绿色为六边形面 |
 倒角大二十面体的面 在顶点周围的排布 |
复杂斜方截半大十二面体
[编辑]除了大复杂斜方截半二十面体外,还有一种退化的小双三斜三十二面体刻面多面体[8],其为复杂斜方截半大十二面体[9],其外观与双三斜十二面体和五复合立方体所形成的复合几何形状相同[9]。
| 离面(Cantellation)多面体 | 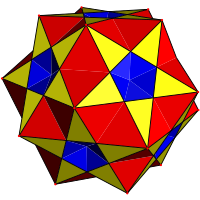 小复杂斜方截半二十面体 |
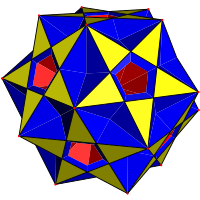 复杂斜方截半大十二面体 |
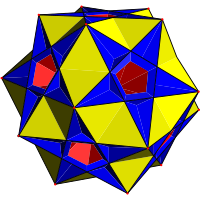 大复杂斜方截半二十面体 | |||
|---|---|---|---|---|---|---|
| 关联多面体 |  大二十面体 |
 大星形十二面体 |
 大十二面体 |
 小星形十二面体 |
 正十二面体 |
 正二十面体 |
参见
[编辑]参考文献
[编辑]- ^ Jim McNeill. Polyhedral "Twisters". orchidpalms.com. [2019-10-05]. (原始内容存档于2019-03-11).
- ^ 2.0 2.1 2.2 2.3 2.4 Klitzing, Richard. sicdatrid, Polytopes & their Incidence Matrices. bendwavy.org. [2019-10-05]. (原始内容存档于2016-03-25).
- ^ Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P., Uniform polyhedra, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 1954, 246: 401–450, ISSN 0080-4614, JSTOR 91532, MR 0062446, doi:10.1098/rsta.1954.0003
- ^ 4.0 4.1 Klitzing, Richard. gicdatrid, Polytopes & their Incidence Matrices. bendwavy.org. [2019-10-05]. (原始内容存档于2016-03-24).
- ^ Klitzing, Richard. polyhedra. bendwavy.org. [2019-10-05]. (原始内容存档于2018-07-07).
- ^ Weisstein, Eric W. (编). Expansion. at MathWorld--A Wolfram Web Resource. Wolfram Research, Inc. (英语).
- ^ Deza, M. and Grishukhin, V. and Shtogrin, M. Scale-isometric Polytopal Graphs in Hypercubes and Cubic Lattices: Polytopes in Hypercubes and Zn?. Imperial College Press. 2004. ISBN 9781860944215. LCCN 2004445213.
- ^ Klitzing, Richard. sidtid, Polytopes & their Incidence Matrices. bendwavy.org. [2019-10-05]. (原始内容存档于2016-03-24).
- ^ 9.0 9.1 Klitzing, Richard. cadditradid, Polytopes & their Incidence Matrices. bendwavy.org. [2019-10-05]. (原始内容存档于2016-03-25).