克魯斯卡爾坐標系(或稱作克魯斯卡爾-塞凱賴什坐標系,英文Kruskal coordinates或Kruskal-Szekeres coordinates)是在史瓦西度規下建立的一種坐標系,名稱來自於美國數學物理學家馬丁·克魯斯卡爾(Martin Kruskal)和匈牙利-澳大利亞數學家喬治·塞凱賴什。這種坐標系的優點在於它能夠涵蓋整個時空流形,使得奇異點之外的所有點在坐標系中都存在定義,也就是說它能夠將原有的在球坐標系下的史瓦西度規最大限度地推廣到整個時空中。
 圖1——Kruskal坐標
圖1——Kruskal坐標
考慮在球坐標系下的史瓦西度規

其中

是二維球面 的線元。
的線元。
將時間坐標 和徑向坐標
和徑向坐標 做如下代換:
做如下代換:
- 對於視界外部
 的區域,
的區域,


- 對於視界內部
 的區域,
的區域,


在這些坐標下,史瓦西度規由下式給出:

其中 的定義被隱含在
的定義被隱含在

或等價於

其中 是朗伯W函數。
是朗伯W函數。
這組由 構成的坐標系稱作Kruskal坐標系,有時也稱作Kruskal-Szekeres坐標系。
構成的坐標系稱作Kruskal坐標系,有時也稱作Kruskal-Szekeres坐標系。
 圖2——藍色的雙曲線族表示徑向坐標
圖2——藍色的雙曲線族表示徑向坐標 為常數的面
為常數的面
史瓦西黑洞的視界位於 ,此時
,此時

的右面為零,從而有

即史瓦西黑洞的視界在T-R平面上是兩條45°的對角線。
對於一般的常數 ,可以得到
,可以得到

即它們是T-R平面上的一組雙曲線。
對於一般的常數 ,
,

它們是通過原點的斜率為 的直線。注意到當
的直線。注意到當 時
時 ,從而等價於
,從而等價於 的情形。這表明
的情形。這表明 和
和 描述的是同一個面。
描述的是同一個面。
如果像上節所述那樣將時空圖畫到T-R平面上就得到了像右面圖1所示的Kruskal圖。Kruskal圖上的每一點都代表了一個二維球面。從圖中可以看到:
- 徑向坐標
 可以從正無窮大連續變化到零,中間經過視界
可以從正無窮大連續變化到零,中間經過視界 。這個連續變化對應著圖2中藍色的雙曲線族,其中經過R軸的雙曲線對應著
。這個連續變化對應著圖2中藍色的雙曲線族,其中經過R軸的雙曲線對應著 的情形,經過T軸的雙曲線對應著
的情形,經過T軸的雙曲線對應著 的情形,雙曲線的兩條漸近線對應著
的情形,雙曲線的兩條漸近線對應著 的視界。
的視界。 對應著黑洞的奇異點,而在那以外的部分(圖2中的灰色區域)時間和空間坐標都沒有定義。
對應著黑洞的奇異點,而在那以外的部分(圖2中的灰色區域)時間和空間坐標都沒有定義。
- 時間坐標
 可以從負無窮大連續變化到正無窮大,其範圍涵蓋了兩條漸近線(兩條45°的對角線)所夾的包含R軸的部分,即在這範圍內通過原點的所有直線。R軸對應著時間坐標
可以從負無窮大連續變化到正無窮大,其範圍涵蓋了兩條漸近線(兩條45°的對角線)所夾的包含R軸的部分,即在這範圍內通過原點的所有直線。R軸對應著時間坐標 的直線。
的直線。
- 在Kruskal坐標下,R具有從負無窮大到正無窮大的連續定義,T也一樣,但兩者在灰色區域仍然沒有定義。
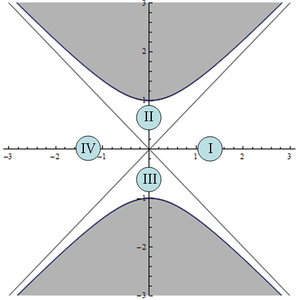 圖3——最大延伸的史瓦西解所包含的四個不同時空
圖3——最大延伸的史瓦西解所包含的四個不同時空
對於球坐標系下的史瓦西解而言,存在物理意義的徑向坐標的範圍是 ,且
,且 ;但從上節我們已經看到在Kruskal坐標系中,在避免撞上奇異點
;但從上節我們已經看到在Kruskal坐標系中,在避免撞上奇異點 的前提下所允許的R的範圍是從負無窮大到正無窮大,並且
的前提下所允許的R的範圍是從負無窮大到正無窮大,並且 。在Kruskal圖中所描述的史瓦西解被稱作最大延伸的史瓦西解(Maximally Extended Schwarzchild Solution),從圖3中可以看到它包含有通過視界
。在Kruskal圖中所描述的史瓦西解被稱作最大延伸的史瓦西解(Maximally Extended Schwarzchild Solution),從圖3中可以看到它包含有通過視界 分割的四個不同的時空:
分割的四個不同的時空:
| I
|
我們的宇宙 |
 且 且  |

|
| II
|
黑洞視界內部 |
 且 且  |

|
| III
|
白洞視界內部 |
 且 且  |

|
| IV
|
鏡像宇宙 |
 且 且  |

|
- 區域I——史瓦西幾何中
 的時空,也就是黑洞視界以外,我們的漸進平直時空。
的時空,也就是黑洞視界以外,我們的漸進平直時空。
- 區域II——史瓦西幾何中
 的時空,也就是史瓦西黑洞的內部。任何從區域I經過視界
的時空,也就是史瓦西黑洞的內部。任何從區域I經過視界 到達區域II的物體都無法返回區域I,並且它們的最終命運都是撞上奇異點
到達區域II的物體都無法返回區域I,並且它們的最終命運都是撞上奇異點 。
。
- 區域III——史瓦西幾何中
 區域的時間反演,也就是說物體可以從區域III經過視界到達區域I,但它們都無法返回區域III。這就是理論上一個白洞的物理概念:白洞具有一個類似於宇宙大爆炸那樣的過去的奇異點,同時具有過去的視界(相對於區域II中未來的奇異點和未來的視界)。
區域的時間反演,也就是說物體可以從區域III經過視界到達區域I,但它們都無法返回區域III。這就是理論上一個白洞的物理概念:白洞具有一個類似於宇宙大爆炸那樣的過去的奇異點,同時具有過去的視界(相對於區域II中未來的奇異點和未來的視界)。
- 區域IV——同樣作為
 的漸近平直時空,卻不能通過時間流逝或反演從區域I到達區域IV,或者反過來從區域IV到達區域I,這是我們宇宙的一個鏡像。在理論上,能夠在這兩個宇宙間建立聯繫的方法是蟲洞(愛因斯坦-羅森橋)。假設將Kruskal圖上所描述的時空以T為常數切成多個類空的表面,則在史瓦西幾何中能夠在短時間內存在一個連接兩個漸進平直時空的蟲洞。但在理論上,這個蟲洞的敞開時間太短以至於任何類時的觀察者都無法通過蟲洞到達鏡像時空中。
的漸近平直時空,卻不能通過時間流逝或反演從區域I到達區域IV,或者反過來從區域IV到達區域I,這是我們宇宙的一個鏡像。在理論上,能夠在這兩個宇宙間建立聯繫的方法是蟲洞(愛因斯坦-羅森橋)。假設將Kruskal圖上所描述的時空以T為常數切成多個類空的表面,則在史瓦西幾何中能夠在短時間內存在一個連接兩個漸進平直時空的蟲洞。但在理論上,這個蟲洞的敞開時間太短以至於任何類時的觀察者都無法通過蟲洞到達鏡像時空中。
- Misner, Thorne, Wheeler. Gravitation. W H Freeman and Company. 1973. ISBN 0-7167-0344-0 (英语). 第32.6節
- Sean M. Carroll. Spacetime and Geometry: An Introduction to General Relativity (Hardcover). Benjamin Cummings. 2003. ISBN 978-0805387322 (英语). 第5.7節










































