冪

此條目的主題是代數概念。關於幾何定理，請見「圓冪定理」。

bn
記號
底數$b$ 與 指數$n$

在數學中，重複連乘的運算叫做乘方，乘方的結果稱為 冪（英語：mathematical power，power）；由此，若 $n$ 為正整數，$n$ 個相同的數 $b$ 連續相乘（即 $b$ 自乘 $n$ 次），就可將 $b^{n}$ 看作乘方的結果 ——「冪」。

$b^{n}=\underbrace {b\times \cdots \times b} _{n}$

冪運算（exponentiation）又稱指數運算、取冪，是數學運算，表達式為 $b^{n}$，讀作「$b$ 的 $n$ 次方」或「$b$ 的 $n$ 次冪」。其中，$b$ 稱為底數，而 $n$ 稱為指數，通常指數寫成上標，放在底數的右邊。在純文字格式等不能用上標的情況，例如在編程語言或電子郵件中，$b^{n}$ 通常寫成 b^n 或 b**n；也可視為超運算，記為 b[3]n；亦可以用高德納箭號表示法，寫成 b↑n。

當指數為 1 時，通常不寫出來，因為運算出的值和底數的數值一樣；指數為 2 時，可以讀作「$b$ 的平方」；指數為 3 時，可以讀作「$b$ 的立方」。

由於在十進制中，十的冪很容易計算，只需在後面加零即可，所以科學記數法藉此簡化記錄的數字；二的冪則在計算機科學中相當重要。

起始值 1（乘法的單位元素）乘上底數（$b$）自乘指數（$n$）這麼多次。這樣定義了後，很易想到如何一般化指數 0 和負數的情況：指數是零時，底數不為零，冪均為一（即除 0 外，所有數的 0 次方都是 1 ）；指數是負數時，就等於重複除以底數（或底數的倒數自乘指數這麼多次），即：

$b^{0}=1\qquad (b\neq 0)$

$b^{-n}={1 \over \underbrace {b\times \cdots \times b} _{n}}={\frac {1}{b^{n}}}=\left({\frac {1}{b}}\right)^{n}\qquad (b\neq 0)$。

若以分數為指數的冪，則定義：

$b^{\frac {n}{m}}={\sqrt[{m}]{b^{n}}}$，

即 $b$ 的 $n$ 次方再開 $m$ 次方根。

0的0次方（$0^{0}$）目前沒有數學家給予正式的定義；在部分數學領域中，如組合數學，常用的慣例是定義為 1 。

此外，當 $n$ 是複數，且 $b$ 是正實數時，

$b^{n}=\exp(n\ln(b))$

exp 是指數函數，而 ln 是自然對數。

重要的恆等式

運算法則

• 同底數冪相乘，底數不變，指數相加：

$a^{m}\times a^{n}=a^{m+n}$

• 同底數冪相除，底數不變，指數相減：

$a^{m}\div a^{n}=a^{m-n}$

• 同指數冪相除，指數不變，底數相除($b$不為0)：

${\frac {a^{n}}{b^{n}}}=\left({\frac {a}{b}}\right)^{n}$

其他等式

• $x^{\frac {m}{n}}={\sqrt[{n}]{x^{m}}}$
• $x^{-m}={\frac {1}{x^{m}}}\qquad (x\neq 0)$
• $x^{0}=1\qquad (x\neq 0)$
• $x^{1}=x\,\!$
• $x^{-1}={\frac {1}{x}}\qquad (x\neq 0)$

運算律

加法和乘法存在交換律，比如：$2+3=5=3+2$，$2\times 3=6=3\times 2$，但是冪的運算不存在交換律，$2^{3}=8$，但是$3^{2}=9$。

同樣，加法和乘法存在結合律，比如：$(2+3)+4=9=2+(3+4)$，$(2\times 3)\times 4=24=2\times (3\times 4)$。不過，冪運算沒有結合律：$(2^{3})^{4}=8^{4}=4096$，而$2^{(3^{4})}=2^{81}=2,417,851,639,229,258,349,412,352$，所以$(2^{3})^{4}\neq 2^{(3^{4})}$。

但是冪運算仍然有其運算律，稱為指數律：

• $a^{m}\cdot a^{n}=a^{m+n}$
• ${\frac {a^{m}}{a^{n}}}=a^{m-n}$
• $(a^{m})^{n}=a^{mn}$
• ${\sqrt[{n}]{a^{m}}}=a^{\frac {m}{n}}$
• $a^{n}\cdot b^{n}=(a\cdot b)^{n}$
• ${\frac {a^{n}}{b^{n}}}=\left({\frac {a}{b}}\right)^{n}$

整數指數冪

整數指數冪的運算只需要初等代數的知識。

正整數指數冪

表達式$a^{2}=a\cdot a$被稱作$a$的平方，因為邊長為$a$的正方形面積是$a^{2}$。

表達式$a^{3}=a\cdot a\cdot a$被稱作$a$的立方，因為邊長為$a$的正方體體積是$a^{3}$。

所以$3^{2}$讀作「3的平方」，$2^{3}$讀作「2的立方」。

指數表示的是底數反覆相乘多少次。比如$3^{5}=3\times 3\times 3\times 3\times 3=243$，指數是5，底數是3，表示3反覆相乘5次。

或者，整數指數冪可以遞迴地定義成：

$a^{n}={\begin{cases}1&(n=0)\\a\cdot a^{n-1}&(n>0)\\\left({\frac {1}{a}}\right)^{-n}&(n<0)\end{cases}}$

指數是1或者0

注意$3^{1}$表示僅僅1個3的乘積，就等於3。

注意$3^{5}=3\times 3^{4}$，$3^{4}=3\times 3^{3}$，$3^{3}=3\times 3^{2}$，$3^{2}=3\times 3^{1}$，

繼續，得到$3^{1}=3\times 3^{0}=3$，所以$3^{0}=1$

另一個得到此結論的方法是：通過運算法則${\frac {x^{n}}{x^{m}}}=x^{n-m}$

當$m=n$時，$1={\frac {x^{n}}{x^{n}}}=x^{n-n}=x^{0}$

• 任何數的1次方是它本身。

零的零次方

主條目：零的零次方

$0^{0}$ 其實還並未被數學家完整的定義，但部分看法是$0^{0}=1$ ，在程式語言中（python） $0**0=1$

在這裡給出這一種極限的看法

$\lim _{x\to 0^{+}}x^{x}=0^{0}$ 於是，可以求出 x 取值從 1 到 0.0000001 計算得到的值，如圖

負數指數

我們定義任何不為 0 的數 a 的 -1 次方等於它的倒數。

$a^{-1}={\frac {1}{a}}$

對於非零$a$定義

$a^{-n}={\frac {1}{a^{n}}}$,

而$a=0$時分母為 0 沒有意義。

證法一：

根據定義$a^{m}\cdot a^{n}=a^{m+n}$，當$m=-n$時

$a^{-n}\,a^{n}=a^{-n\,+\,n}=a^{0}=1,$

得$a^{-n}\,a^{n}=1$, 所以$a^{-n}={\frac {1}{a^{n}}}$。

證法二：

通過運算法則${\frac {a^{m}}{a^{n}}}=a^{m-n}$

當$m=0$時，可得$a^{-n}=a^{0-n}={\frac {a^{0}}{a^{n}}}={\frac {1}{a^{n}}}$

負數指數$a^{-n}$還可以表示成1連續除以$n$個$a$。比如：

$3^{-4}={\frac {\frac {\frac {\frac {1}{3}}{3}}{3}}{3}}={\frac {1}{81}}={\frac {1}{3^{4}}}$.

特殊數的冪

10的冪

主條目：科學計數法

在十進制的計數系統中，10的冪寫成1後面跟著很多個0。例如：$10^{3}=1000,\ 10^{-3}=0.001$

因此10的冪用來表示非常大或者非常小的數字。如：299,792,458（真空中光速，單位是米每秒），可以寫成 $2.99792458\times 10^{8}$，近似值 $2.998\times 10^{8}$ 或 $3\times 10^{8}$

國際單位制詞頭也使用10的冪來描述特別大或者特別小的數字，比如：詞頭「千」就是 $10^{3}$，詞頭「毫」就是 $10^{-3}$

2的冪

主條目：2的冪

1的冪

1的任何次冪都為1。

0的冪

0的正數冪都等於0。

0的負數冪沒有定義。

任何非0之數的0次方都是1；而0的0次方是懸而未決的，某些領域下常用的慣例是約定為1。但某些教科書表示0的0次方為無意義。也有人主張定義為1。

負1的冪

-1的奇數冪等於-1

-1的偶數冪等於1

指數非常大時的冪

一個大於1的數的冪趨於無窮大，一個小於-1的數的冪趨於負無窮大

當$a>1$，$n\to \infty$，$a^{n}\to \infty$

當$a<-1$，$n\to \infty$，$a^{n}\to -\infty$ 或 $\infty$ , (視乎n 是奇數或偶數)

一個絕對值小於1的數的冪趨於0

當$|a|<1$，$n\to \infty$，$a^{n}\to 0$

1的冪永遠都是1

當$a=1$，$n\to \infty$，$a^{n}\to 1$

如果數a趨於1而它的冪趨於無窮，那麼極限並不一定是上面幾個。一個很重要的例子是：

當$n\to \infty ,\left(1+{\frac {1}{n}}\right)^{n}\to e$

參見e的冪

其他指數的極限參見冪的極限

正實數的實數冪

一個正實數的實數冪可以通過兩種方法實現。

• 有理數冪可以通過N次方根定義，任何非0實數次冪都可以這樣定義
• 自然對數可以被用來通過指數函數定義實數冪

N次方根

從上到下：$x^{\frac {1}{8}},\ x^{\frac {1}{4}},\ x^{\frac {1}{2}},\ x^{1},\ x^{2},\ x^{4},\ x^{8}$

主條目：方根

一個數$a$的$n$次方根是$x$，$x$使$x^{n}=a$。

如果$a$是一個正實數，$n$是正整數，那麼方程式$x^{n}=a$只有一個正實數根。 這個根被稱為$a$的$n$次方根，記作：${\sqrt[{n}]{a}}$，其中${\sqrt {\ }}$叫做根號。或者，$a$的$n$次方根也可以寫成$a^{\frac {1}{n}}$. 例如$4^{\frac {1}{2}}=2,\ 8^{\frac {1}{3}}=2$

當指數是${\frac {1}{2}}$時根號上的2可以省略，如：${\sqrt {4}}=4^{\frac {1}{2}}={\sqrt[{2}]{4}}=2$

有理數冪

有理數指數冪定義為

$a^{\frac {m}{n}}=(a^{m})^{\frac {1}{n}}={\sqrt[{n}]{a^{m}}}$

e的冪

主條目：指數函數

這個重要的數學常數e，有時叫做歐拉數，近似2.718，是自然對數的底。它提供了定義非整數指數冪的一個方法。 它是從以下極限定義的：

$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

指數函數的定義是：

$e^{x}=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}$

可以很簡單地證明e的正整數k次方$e^{k}$是：

$e^{k}=\left[\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}\right]^{k}$

$=\lim _{n\to \infty }\left(1+{\frac {k}{n\cdot k}}\right)^{n\cdot k}$

$=\lim _{n\cdot k\to \infty }\left(1+{\frac {k}{n\cdot k}}\right)^{n\cdot k}$

$=\lim _{m\to \infty }\left(1+{\frac {k}{m}}\right)^{m}$

實數指數冪

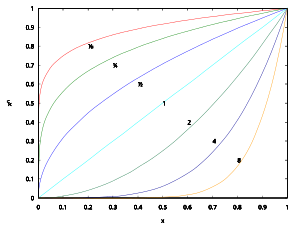
y = b^x對各種底數b的圖像，分別為綠色的10、紅色的e、藍色的2和青色的1/2。

因為所有實數可以近似地表示為有理數，任意實數指數x可以定義成：

$b^{x}=\lim _{r\to x}b^{r},$

例如：

$x\approx 1.732$

於是

$5^{x}\approx 5^{1.732}=5^{\frac {433}{250}}={\sqrt[{250}]{5^{433}}}\approx 16.241$

實數指數冪通常使用對數來定義，而不是近似有理數。

自然對數$\ln {x}$是指數函數$e^{x}$的反函數。 它的定義是：對於任意$b>0$，滿足

$b=e^{\ln b}$

根據對數和指數運算的規則：

$b^{x}=(e^{\ln b})^{x}=e^{x\cdot \ln b}$

這就是實數指數冪的定義：

$b^{x}=e^{x\cdot \ln b}\,$

實數指數冪$b^{x}$的這個定義和上面使用有理數指數和連續性的定義相吻合。對於複數，這種定義更加常用。

負實數的實數冪

如果$a$是負數且$n$是偶數，那麼$x=a^{n}$是正數。如果$a$是負數且$n$是奇數，那麼$x=a^{n}$是負數。

使用對數和有理數指數都不能將$a^{k}$（其中$a$是負實數，$k$實數）定義成實數。在一些特殊情況下，給出一個定義是可行的：負指數的整數指數冪是實數，有理數指數冪對於$a^{\frac {m}{n}}$（$n$是奇數）可以使用$n$次方根來計算，但是因為沒有實數$x$使$x^{2}=-1$，對於$a^{\frac {m}{n}}$（$n$是偶數）時必須使用虛數單位$i$。

使用對數的方法不能定義$a\leq 0$時的$a^{k}$為實數。實際上，$e^{x}$對於任何實數$x$都是正的，所以$\ln(a)$對於負數沒有意義。

使用有理數指數冪來逼近的方法也不能用於負數$a$因為它依賴於連續性。函數$f(r)=a^{r}$對於任何正的有理數$a$是連續的，但是對於負數$a$，函數$f$在有些有理數$r$上甚至不是連續的。

例如：當$a=-1$，它的奇數次根等於-1。所以如果$n$是正奇數整數，$-1^{\frac {m}{n}}=-1$當$m$是奇數，$-1^{\frac {m}{n}}=1$當$m$是偶數。雖然有理數$q$使$-1^{q}=1$的集合是稠密集，但是有理數$q$使$-1^{q}=-1$的集合也是。所以函數$-1^{q}$在有理數體不是連續的。

因此，如果要求負實數的任意實數冪，必須將底數和指數看成複數，按複數的正實數冪或複數的複數冪方法計算。

正實數的複數冪

e的虛數次冪

主條目：指數函數

指數函數e^z可以通過(1 + z/N)^N當N趨於無窮大時的極限來定義，那麼e^iπ就是(1 + iπ/N)^N的極限。在這個動畫中n從1取到100。(1 + iπ/N)^N的值通過N重複增加在複數平面上展示，最終結果就是(1 + iπ/N)^N的準確值。可以看出，隨著N的增大，(1 + iπ/N)^N逐漸逼近極限-1。這就是歐拉公式。

複數運算的幾何意義和e的冪可以幫助我們理解$e^{ix}$（$x$是實數），即純虛數指數函數。想像一個直角三角形$(0,1,1+{\frac {ix}{n}})$（括號內是複數平面內三角形的三個頂點），對於足夠大的$n$，這個三角形可以看作一個扇形，這個扇形的中心角就等於${\frac {x}{n}}$弧度。對於所有$k$，三角形$(0,(1+{\frac {ix}{n}})^{k},(1+{\frac {ix}{n}})^{k+1})$互為相似三角形。所以當$n$足夠大時$(1+{\frac {ix}{n}})^{n}$的極限是複數平面上的單位圓上$x$弧度的點。這個點的極坐標是$(r,\theta )=(1,x)$，直角坐標是$(\cos x,\sin x)$。所以$e^{ix}=\cos x+i\sin x$，而這個函數可以稱為純虛數指數函數。這就是歐拉公式，它通過複數的意義將代數學和三角學聯繫起來了。

等式$e^{z}=1$的解是一個整數乘以$2i\pi$：

$\{z:e^{z}=1\}=\{2k\pi i:k\in \mathbb {Z} \}.$

更一般地，如果$e^{b}=a$，那麼$e^{z}=a$的每一個解都可以通過將$2i\pi$的整數倍加上$b$得到：

$\{z:e^{z}=a\}=\{b+2k\pi i:k\in \mathbb {Z} \}.$

這個複指數函數是一個有週期$2i\pi$的週期函數。

更簡單的：$e^{i\pi }=-1;\ e^{x+iy}=e^{x}(\cos y+i\sin y)$。

三角函數

主條目：歐拉公式

根據歐拉公式，三角函數餘弦和正弦是：

$\cos z={\frac {e^{i\cdot z}+e^{-i\cdot z}}{2}}\qquad \sin z={\frac {e^{i\cdot z}-e^{-i\cdot z}}{2\cdot i}}$

歷史上，在複數發明之前，餘弦和正弦是用幾何的方法定義的。上面的公式將複雜的三角函數的求和公式轉換成了簡單的指數方程式

$e^{i\cdot (x+y)}=e^{i\cdot x}\cdot e^{i\cdot y}.\,$

使用了複數指數冪之後，很多三角學問題都能夠使用代數方法解決。

e的複數指數冪

$e^{x+iy}$可以分解成$e^{x}\cdot e^{iy}$。其中$e^{x}$是$e^{x+iy}$的模，$e^{iy}$決定了$e^{x+iy}$的方向

正實數的複數冪

如果$a$是一個正實數，$z$是任何複數，$a^{z}$定義成$e^{z\cdot \ln(a)}$，其中$x=\ln(a)$是方程式$e^{x}=a$的唯一解。所以處理實數的方法同樣可以用來處理複數。

例如：

$2^{i}=e^{i\cdot \ln(2)}=\cos {\ln 2}+i\cdot \sin {\ln 2}=0.7692+0.63896i$

${{e}^{i}}=0.5403023+0.841471i$

${{10}^{i}}=-0.6682015+0.7439803i$

$(e^{2\pi })^{i}=535.49^{i}=1$

複數的複數冪

複數的虛數冪

讓我們從一個簡單的例子開始：計算$\left(1+i\right)^{i}$。

${\begin{aligned}\left(1+i\right)^{i}&=\left[{\sqrt {2}}\left({\frac {\sqrt {2}}{2}}+{\frac {\sqrt {2}}{2}}i\right)\right]^{i}\\&=\left({\sqrt {2}}e^{{\tfrac {\pi }{4}}i}\right)^{i}\\&=e^{-{\tfrac {\pi }{4}}}{\sqrt {2}}^{i}\\&=e^{-{\tfrac {\pi }{4}}}\cos {\frac {\ln 2}{2}}+ie^{-{\tfrac {\pi }{4}}}\sin {\frac {\ln 2}{2}}\\\end{aligned}}$

其中${\sqrt {2}}^{i}$的得法參見上文正實數的複數冪

複數的複數冪

類似地，在計算複數的複數冪時，我們可以將指數的實部與虛部分開以進行冪計算。例如計算$\left(1+i\right)^{2+i}$：

${\begin{aligned}\left(1+i\right)^{2+i}&=\left(1+i\right)^{2}\left(1+i\right)^{i}\\&=2ie^{-{\tfrac {\pi }{4}}}\left(\cos {\frac {\ln 2}{2}}+i\sin {\frac {\ln 2}{2}}\right)\\&=-2e^{-{\tfrac {\pi }{4}}}\sin {\frac {\ln 2}{2}}+2ie^{-{\tfrac {\pi }{4}}}\cos {\frac {\ln 2}{2}}\\\end{aligned}}$

一般情況

複數的複數冪必須首先化為底數為$e$的形式：

$w^{z}=e^{z\ln w}$

又，由複數的極坐標表示法：

$w=re^{i\theta }$

故

$w^{z}=e^{z\ln(w)}=e^{z(\ln(r)+i\theta )}$。

然後，使用歐拉公式處理即可。

由於複數的極坐標表示法中，輻角$\theta$的取值是具有週期性的，因此複數的複數冪在大多數情況下是多值函數。不過實際應用中，為了簡便起見，輻角都只取主值，從而使冪值唯一。

在函數中

當函數名後有上標的數（即函數的指數），一般指要重複它的運算。例如$f^{3}(x)$即$f(f(f(x)))$。特別地，$f^{-1}(x)$指$f(x)$的反函數。

但三角函數的情況有所不同，一個正指數應用於函數的名字時，指答案要進行乘方運算，而指數為-1時則表示其反函數。例如：$(\sin x)^{-1}$表示$\csc x$。因此在三角函數時，使用$\sin ^{-1}x$來表示$\sin x$的反函數$\arcsin x$。

計算自然數（正整數）$n$的$a^{n}$的算法

最快的方式計算$a^{n}$，當$n$是正整數的時候。它利用了測試一個數是奇數在計算機上是非常容易的，和通過簡單的移所有位向右來除以2的事實。

在C/C++語言中，你可以寫如下算法：

double power(double a, unsigned int n)
{
    double y = 1;
    double f = a;
    while (n > 0) {
       if (n % 2 == 1) y *= f;
       n >>= 1;
       f *= f;
    }
    return y;
}

此算法的時間複雜度為$\mathrm {O} (\log n)\!$，比普通算法快（a自乘100次，時間複雜度為$\mathrm {O} (n)\!$），在$n$較大的時候更為顯著。

例如計算$a^{100}$，普通算法需要算100次，上述算法則只需要算7次。若要計算$a^{n}(n<0)$可先以上述算法計算$a^{|n|}$，再作倒數。

另見

• 迭代冪次

外部連結

• 指數的歷史