大斜方截角立方體堆砌
外觀
| 大斜方截角立方體堆砌 | |
|---|---|
 | |
| 類型 | 均勻堆砌 |
| 維度 | 3 |
| 對偶多胞形 | 絹英鍥形體堆砌 |
| 類比 | 截角正方形鑲嵌 |
| 數學表示法 | |
| 考克斯特符號 | |
| 考克斯特記號 | [[4,3,4]] |
| 纖維流形記號 | 8o:2 |
| 施萊夫利符號 | t0,1,2,3{4,3,4} |
| 性質 | |
| 胞 | t {3 4} t {2,8} |
| 面 | {4} {6} {8} |
| 組成與佈局 | |
| 頂點圖 | 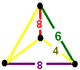 絹英鍥形體 |
| 對稱性 | |
| 對稱群 | |
| 空間群 | Im3m (229) |
| 考克斯特群 | [4,3,4], |
| 特性 | |
| 頂點正 | |
在幾何學中,大斜方截角立方體堆砌是一種歐幾里得三維空間的半正堆砌,是由大斜方截半立方體和正八角柱以1:3的比例堆砌而成。
康威稱大斜方截角立方體堆砌為b-tCO-trille[1],因為它可以藉由對應的康威多面體變換而構造出來。其可以視為立方體堆砌經過「大斜方截半」變換構造而來,也可以視為由大斜方截半立方體堆砌而得,但大斜方截半立方體無法單獨堆砌,必須和其他多面體一起堆砌,而大斜方截角立方體堆砌是大斜方截半立方體和正八角柱共同堆砌而得。
對稱性
[編輯]由於大斜方截角立方體堆砌是由立方體堆砌為種子做大斜方截半變換而構造出來,因此其會保有種子(立方體堆砌)的部分或全部的對稱性,因此大斜方截角立方體堆砌具有對稱性,空間對稱性則為Im3m,與立方體堆砌的Pm3m有所差異,但經過表面塗色,![]()
![]()
![]()
![]()
![]()
![]()
![]() ,其對稱性即可變為Pm3m空間平移對稱性。
,其對稱性即可變為Pm3m空間平移對稱性。
表面塗色
[編輯]大斜方截角立方體堆砌有兩種不同的表面塗色,胞的塗色模式不同,對稱性也會不同。在考克斯特記號的形式有兩種不同的方法能在大斜方截半立方體和正八角柱塗上顏色。在考克斯特記號與所述第一和最後一個分支能使對稱性加倍。這可以顯示用一種顏色塗滿所有大斜方截半立方體和正八角柱胞的對稱性。
| 對稱性 | , [4,3,4] | ×2, [[4,3,4]] |
|---|---|---|
| 空間群 | Pm3m (221) | Im3m (229) |
| 纖維流形 | 4−:2 | 8o:2 |
| 表面塗色 | 
|

|
| 考克斯特符號 | ||
| 頂點圖 | 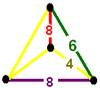
|
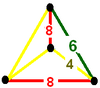
|
參考文獻
[編輯]- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (包含11個凸半正鑲嵌、28個凸半正堆砌、和143個凸半正四維砌的全表)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication參與編輯, 1995, ISBN 978-0-471-01003-6 http://www.wiley.com/WileyCDA/WileyTitle/productCd-0471010030.html (頁面存檔備份,存於網際網路檔案館)
- (22頁) H.S.M.考克斯特, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 半正空間鑲嵌)
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- ^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)





